Photo by Jonathan Petersson on Unsplash

I recently came across an interesting probability question from Nate Rosidi, maintainer of the data science prep site Strata Scratch. This question was asked by FiveThirtyEight and goes like this:

You start with a fair 6-sided die and roll it six times, recording the results of each roll. You then write these numbers on the six faces of another, unlabeled fair die. For example, if your six rolls were 3, 5, 3, 6, 1 and 2, then your second die wouldn’t have a 4 on it; instead, it would have two 3s.

Next, you roll this second die six times. You take those six numbers and write them on the faces of yet another fair die, and you continue this process of generating a new die from the previous one.

Eventually, you’ll have a die with the same number on all six faces.

What is the average number of rolls it will take to reach this state?"

Nathan attempted using a Markov Model defining all probability states that could occur between dice rolls. In his own words:

I couldn’t figure out the trick to this problem, so I spent way too long calculating the whole 11 x 11 transition probability matrix (there are 11 unique states the die can be in, e.g. 1 number with 3 sides, and 3 numbers with one side) and then using python to solve the system of equations. The answer is ~9.66, but there must be a more elegant way.

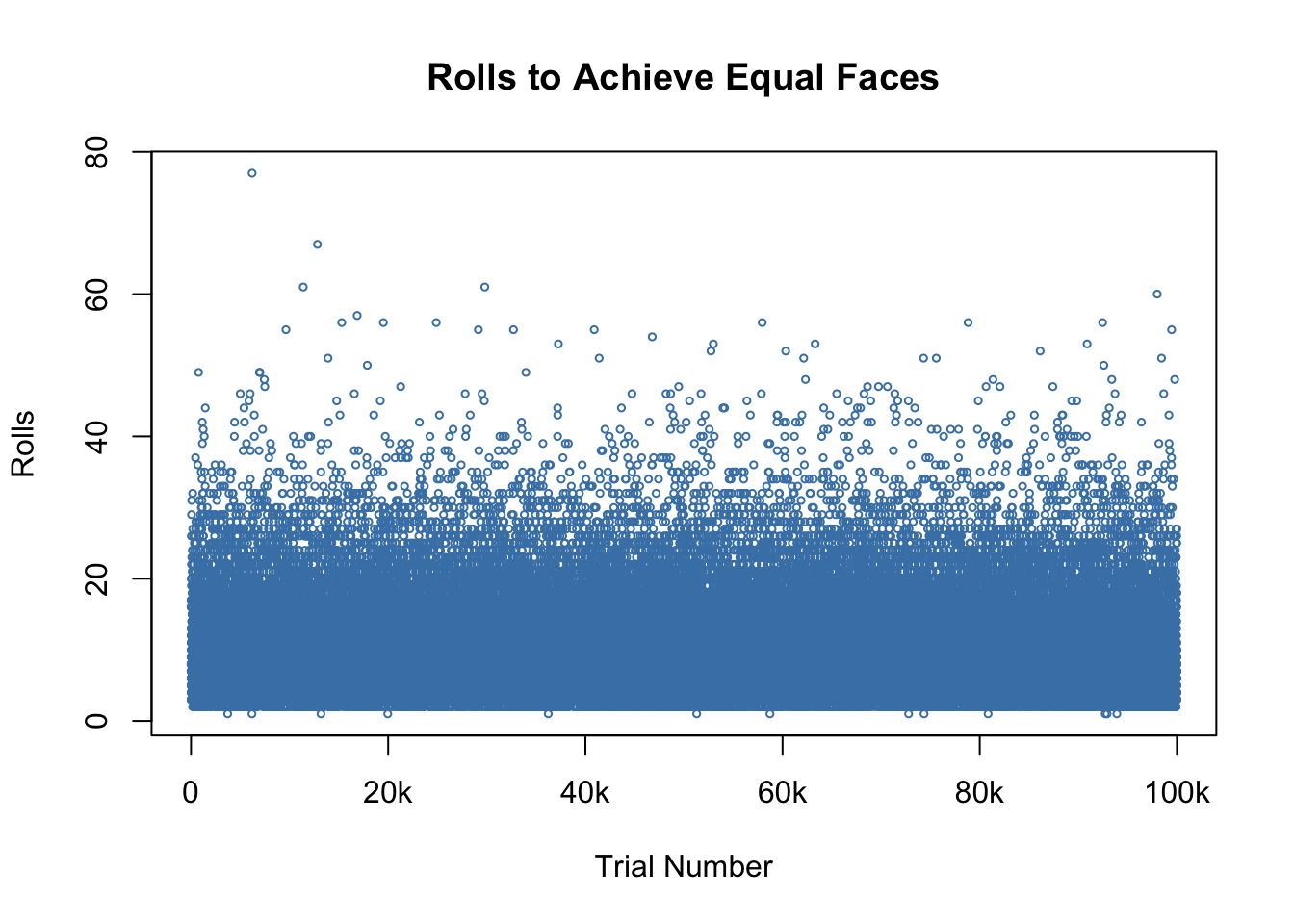
I thought how I would replicate it, but then remembered simulation would be a much better (and faster) idea. To that end, I made an R script that simulates 100,000 trials. Each trial consists of rolling the dice until arriving at the desired outcome of all six faces being equal.

# reproducibility
set.seed(42)
# define number of trials to be 100,000
num_trials <- 1:100000
# a vector that stores the number of rolls it takes for each trial to arrive at an equal number of faces
rolls_to_eq_outcome <- c()

for (i in num_trials){ # for each trial
  # initialze a counter that keeps track of how many rolls it took to get all equal faces for that trial
  num_to_equal_faces <- 0
  # the default die faces
  dice <- 1:6
  # start tracking if a roll has equal faces
  while (TRUE) {
    # roll the dice
    roll_outcome <- sample(dice, size=6, replace = T)
    # increment counter
    num_to_equal_faces <- num_to_equal_faces + 1
    # if the six faces are not all equal...
    if (length(unique(roll_outcome)) != 1) {
      # update faces of the die to the latest outcome and roll again
      dice <- roll_outcome
    }
    # if you do get a roll with all six faces being the same...
    if (length(unique(roll_outcome)) == 1){
      # append the number of rolls it took to the rolls_to_eq_outcome
      rolls_to_eq_outcome <- append(rolls_to_eq_outcome, num_to_equal_faces)
      break
    }
  }
}
  
paste0("Average number of rolls to get equal faces: ", mean(rolls_to_eq_outcome))

[1] "Average number of rolls to get equal faces: 9.66755"

Here’s a breakdown of the logic:

1. Define a dice variable to be a vector with values 1 through 6 like any standard die. This vector represents each of the six faces on the die.

2. For each trial, have a counter variable num_to_equal_faces that keeps track of how many times the die is rolled

3. Keep rolling the die (and updating dice) so long as each outcome doesn’t produce equal faces

4. Once you get a roll with all equal faces, cease incrementing num_to_equal_faces and append it’s latest value to rolls_to_equal_outcome, which keeps track of how many rolls it took for each trial to achieve equal faces

Notice my answer matches Nate’s. I’m satisfied 😀 It’s interesting that some of the trials took an unusually long time to yield equal faces - one of the them took nearly 80 rolls!